1.3: The Phase Line

Open In Colab

Reading: Notes on Diffy Q’s Section 1.6

Analyzing Autonomous DEs: Spotted Owls

A group of biologists are making predictions about the spotted owl population in a forest in the Pacific Northwest. The autonomous differential equation the scientist use to model the spotted owl population is

\[\frac{dP}{dt}=\frac{P}{2}\left(1-\frac{P}{5}\right)\left(\frac{P}{8}-1\right),\]

where \(P\) is in hundreds of owls and \(t\) is in years. The issue is that the current number of owls is only approximately known.

Question 1:

Suppose the scientists estimate that currently \(P\) is about 5 (i.e. there are currently about 500 owls in the forest). Since 5 is only an estimate, they make long-term predictions of the owl population for the initial conditions \(P = 4.9\), \(P = 5.0\), and \(P = 5.1\).

Without using Python or any other technology, determine the long-term predictions for these initial conditions based on the differential equation. Will slightly different initial conditions yield only slightly different long-term predictions, or will they be radically different? Carry out a similar analysis if the current number of owls is somewhere near 800 owls.

Solution to Question 1:






Question 2:

Give a one dimensional representation, without words, that would describe all solutions to the differential equation.

Solution to Question 2:






Phase Lines

A phase line is the standard one-dimensional diagram that depicts the qualitative behavior of solutions to an autonomous differential equation.

Question 3:

Label the dots and add arrows to the figure below to represent all solutions to the differential equation in Question 1.

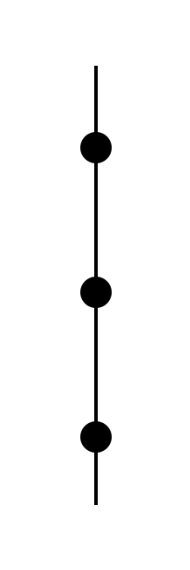
Blank Phase Line

Solution to Question 3:





Question 4:

For the differential equation in questions 1 thru 3 there are three equilibrium solutions. Recall that equilibrium solutions are constant functions that satisfy the differential equation. How do the other solution functions near each equilibrium solution behave in the long term? If you were to label each of these equilibrium solutions based on the way in which nearby solutions behave, what terms would you use and why?

Solution to Question 4:





Question 5:

Create an autonomous differential equation that has exactly two equilibrium solutions: \(y(t)=3\) is a stable equilibrium and \(y(t) = -4\) is an unstable equilibrium.

Solution to Question 5:






Creative Commons License Information

Creative Commons License
Exploring Differential Equations by Adam Spiegler is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Based on a work at https://github.com/CU-Denver-MathStats-OER/ODEs and original content created by Rasmussen, C., Keene, K. A., Dunmyre, J., & Fortune, N. (2018). Inquiry oriented differential equations: Course materials. Available at https://iode.sdsu.edu.